استفاده از تحلیل دینامیکی طیفی نه تنها برای ساختمان های دارای نامنظمی و سازه های با ارتفاع نسبتا زیاد اجباری است بلکه باعث اقتصادی شدن پروژه نیز می شود. با توجه به اینکه در اکثر شهرهای کشوردر حال حاضر تمایل بیشتر کارفرمایان به بلندمرتبه سازی ساختمان ها وجود دارد و با توجه به محدودیت هایی که جهت تحلیل استاتیکی سازه ها وجود دارد، لازم است مهندسین عمران و خصوصا مهندسین طراح سازه به تحلیل دینامیکی طیفی به عنوان یکی از انواع روش های تحلیل سازه مسلط باشند. به همین منظور در این مقاله به بررسی صفر تا صد تحلیلی دینامیکی طیفی و انجام آن در نرم افزار ایتبس می پردازیم پس تا آخر مقاله با ماه همراه باشید.
تحلیل طیفی چیست؟
تحلیل طیفی به عنوان یکی از متداول ترین روش ها جهت افزایش دقت تحلیل خطی سازه مورد استفاده قرار می گیرد. درحقیقت این روش برخی از کاستی های روش تحلیل استاتیکی معادل را پوشش داده و می تواند برآورد واقع بینانه تری از توزیع نیروی زلزله در سازه ایجاد کند. تحلیل دینامیکی خطی می تواند به دو روش تحلیل طیفی و تحلیل تاریخچه زمانی خطی انجام شود. در این روش سازه با فرض رفتار خطی و با اعمال اثر حرکات زمین در تراز پایه آن، تحلیل می شود.
با توجه به اینکه استفاده از روش تحلیل دینامیکی با توجه به برخی تخفیفات آیین نامه در این روش در سازه های منظم و گاهی سازه های نامنظم منجر به سبک سازی سازه نسبت به روش تحلیل استاتیکی می شود؛ و با توجه به برخی محدودیت ها آیین نامه ای در استفاده از تحلیل استاتیکی، در این مقاله به شرح روش آنالیز دینامیکی طیفی و چگونگی انجام این آنالیز در نرم افزار ایتبس خواهیم پرداخت.
آنالیز دینامیکی خطی (Linear Dynamic Procedure- LDP)
روش تحلیل دینامیکی با فرض رفتار خطی مصالح سازه و با استفاده از پاسخ مودهای نوسانی انجام می گیرد.
تحلیل دینامیکی خطی به دو صورت قابل انجام می باشد:
- روش طیفی
- روش تاریخچه زمانی
فرضیات این روش به شرح زیر می باشد:
- رفتار سازه حین رخداد زلزله، به صورت ترکیب خطی از مودهای مختلف سازه می باشد.
- زمان تناوب ارتعاشات سازه در هر مود در طول رخداد زلزله ثابت است.
بر اساس بند 3-4-1-1 استاندارد 2800، ویرایش چهارم، روش تحلیل طیفی به صورت زیر انجام می شود:
- مدل سازه بر اساس رفتار خطی تهیه می شود.
- تحلیل مقادیر ویژه بر روی مدل سازه انجام شده و مشخصات مودهای طبیعی نوسان آن تعیین می گردد.
- حداکثر پاسخ در هر مود با توجه به زمان تناوب آن مود و با استفاده از طیف طرح استاندارد و یا طیف طرح ویژه ساختگاه که با ضریب رفتار (R) کاهش داده شده است به دست می آید.
- از آن جایی که حداکثر پاسخ ها برای مودهای مختلف در یک زلزله به طور همزمان اتفاق نمی افتد؛ بنابر این لازم است که با روش های آماری مختلف پاسخ های کلی حداکثر در اعضا تخمین زده شود. این روش های آماری باید ترکیبی از حداکثر پاسخ مودهای مختلف بوده و آثار اندرکنش احتمالی بین پاسخ مختلف حاصل از مودهای دیگر را در بر گیرد. در این راستا می توان از ترکیب روش جذر مجموع مربعات (SRSS) و یا روش ترکیب مربعی کامل (CQC) جهت تخمین پاسخ کلی سازه استفاده نمود. باید در نظر داشت که ترکیب اثر مودها در ساختمان های نامنظم در پلان و یا در مواردی که زمان تناوب دو یا چند مود سازه به یکدیگر نزدیک باشد باید صرفاً با روش CQC انجام شود.
بر اساس نشریه 360، تعداد مودهای ارتعاش در تحلیل طیفی باید چنان انتخاب شود که جمع درصد مشارکت جرم مؤثر برای هر امتداد زلزله در مودهای انتخاب شده حداقل 90 درصد کل جرم سازه باشد.
لزوم استفاده از تحلیل دینامیکی
هرچند روش های تحلیل استاتیکی معادل نسبت به روش های تحلیل دینامیکی ساده تر بوده و پیچیدگی کمتری دارد، ولی در بسیاری از موارد ویژگی های یک سازه به گونه ای است که از روش تحلیل استاتیکی معادل در مورد آن سازه ایجاد خطا می کند.
با توجه به رابطه ی توزیع نیروی جانبی طبقات، می توان گفت توزیع برش پایه در ارتفاع، در روش تحلیل استاتیکی معادل به وزن هر طبقه و ارتفاع هر طبقه از تراز پایه وابسته است. علاوه بر این پارمتر k نیز در این رابطه تا حدی دقت توزیع نیرو را بالا می برد. این در حالی است که عوامل مختلف دیگری در توزیع نیرو در ارتفاع طبقه نقش دارند؛ که یکی از مهمترین آن ها سختی طبقات نسبت به یکدیگر می باشد. از این رو در صورتی که رفتار جانبی سازه ای عمدتاً تابع وزن و ارتفاع طبقات باشد روش استاتیکی معادل می تواند برآورد قابل قبولی از توزیع نیروی جانبی در ارتفاع داشته باشد. این در حالی است که در بسیاری از سازه ها سختی نسبی طبقات تعیین کننده بوده و نقش به سزایی در توزیع نیروها دارند.
از این رو در این حالت روش های تحلیل دینامیکی به عنوان روشی مناسب جهت تحلیل سازه می باشند. در روش های تحلیل دینامیکی علاوه بر وزن و ارتفاع طبقه، عواملی همچون سختی نسبی طبقات و اثر مودهای بالاتر در توزیع نیروهای جانبی زلزله نقش دارند. بر اساس بند 3-2-2 ویرایش چهارم استاندارد 2800، روش های تحلیل خطی را می توان در کلیه ساختمان ها با هر تعداد طبقه به کار برد.
تنها، روش استاتیکی معادل را می توان در ساختمان های سه طبقه و کوتاه تر از تراز پایه و یا ساختمان های زیر به کار گرفت:
- ساختمان های منظم با ارتفاع کمتر از 50 متر از تراز پایه
- ساختمان های نامنظم با ارتفاع کمتر از 50 متر از تراز پایه که دارای نامنظمی زیاد و شدید پیچشی در پلان نباشند.
- نامنظمی جرمی، نرم و خیلی نرم در ارتفاع نباشند.
بر اساس این بند از استاندارد 2800، از روش تحلیل دینامیکی در تمامی سازها جهت افزایش دقت مدلسازی می توان استفاده کرد؛ اما در سازه هایی که دارای شرایط ذکر شده در این بند نباشند استفاده از روش استاتیکی معادل مجاز نبوده و حتماً باید از روش های تحلیل دینامیکی استفاده نمود.
پیشنهاد آموزشی:دوره آموزش طراحی سازه با ایتبس و سیف | آموزش پروژهمحور سازه فولادی و بتنی
باید در نظر داشت اگرچه بر اساس استاندارد 2800، روش تحلیل استاتیکی معادل در بسیاری از سازه ها از دقت کافی برخوردار است و نیازی به استفاده از تحلیل دینامیکی نمی باشد، اما طراحان حرفه ای سازه در این موارد نیز از تحلیل دینامیکی استفاده می کنند. لازم به ذکر است استفاده از روش تحلیل طیفی علاوه بر این که توزیع نیروها را در سازه منطقی تر می کند و باعث افزایش دقت در طراحی می گردد، می تواند موجب سبک تر شدن طراحی سازه های منظم و در برخی موارد سازه های نامنظم اعم از نامنظمی در ارتفاع و نامنظمی در پلان گردد. این امر به دلیل کاهش میزان برش پایه نسبت به تحلیل استاتیکی می باشد.
تحلیل دینامیکی در ایتبس
در ادامه روند انجام تحلیل دینامیکی ساختمان 7 طبقه اسکلت بتنی نشان داده شده در شکل زیر با استفاده از نرم افزار ایتبس بیان شده است.
آنالیز مودال
جهت انجام تحلیل دینامیکی ابتدا باید ویژگی های مودهای مختلف تعیین شود. در ادامه روند و گام های لازم جهت انجام آنالیز مودال بیان می شود:
تعیین جرم لرزه ای هر طبقه
جهت تعیین جرم مؤثر لرزه ای طبقات از مسیر زیر وارد پنجره ی نشان داده شده در شکل شده و ضرایب الگوی بار جهت محاسبه ی وزن مؤثر لرزه ای به نرم افزار را معرفی می کنیم:
پیشنهاد آموزشی: پکیج جامع قبولی آزمون محاسبات 1404(اینجا کلیک کنید)
Define> Mass Source> Modify/Show Mass Source
بر اساس بند 3-3-1-1 ویرایش چهارم استاندارد 2800، وزن مؤثر لرزه ای شامل مجموع بارهای مرده و وزن تأسیسات ثابت و وزن دیوارهای پارتیشن به اضافه ی درصدی از بار زنده و بار برف، مطابق جدول (3-1) از این استاندارد که در پایین آورده شده است می باشد.
تعیین مودهای ارتعاش سازه
تعداد مودهای ارتعاش سازه برابر با تعداد درجات آزادی سازه می باشد. بنابر این در سازه های معمولی با ارتفاع متوسط هزاران مود ارتعاشی وجود دارد. محاسبه ی خصوصیات این مودها حجم محاسبات را افزایش داده و فرایندی زمان بر می باشد. در صورتی که به طبقات سازه دیافراگم در سقف اختصاص داده شود تعداد مودهای اصلی نوسان به سه برابر تعداد طبقه محدود می شود. بنابراین در این مرحله جهت تعیین تعداد مودهای اصلی نوسان از مسیر زیر وارد پنجره ی نشان داده شده در شکل می شویم.
Define> Modal Case>Modify /Show Case
در اینجا با توجه به اینکه تعداد طبقات سازه 7 طبقه می باشد تعداد مود نوسان را همان گونه که در شکل نشان داده شده است برابر با 21 تعیین کرده ایم.
بارگذاری طیفی
همان گونه که قبلاً نیز اشاره شد یکی از فرضیات روش تحلیل دینامیکی خطی، ثابت بودن زمان تناوب ارتعاشات سازه در هر مود در طول رخداد زلزله می باشد. از این رو با توجه به متفاوت بودن زمان تناوب مودهای مختلف، مقدار ضریب بازتاب ساختمان B برای هر مود متفاوت می باشد. بنابراین برش پایه متناظر با مود i ام به صورت زیر به دست می آید:
با توجه به اینکه در سازه چندین مود با زمان تناوب های مختلف وجود دارد؛ بنابراین با استفاده از نمودار طیف بازتاب، ضریب بازتاب متناسب با مودهای 1 تا i ام که زمان تناوب های آن ها برابر با T1 تا Ti است به دست می آید. مقدار ضریب بازتاب به پارامترهای نوع خاک و میزان لرزه خیزی منطقه وابسته است. در ادامه به چگونگی به دست آوردن نمودار ضریب بازتاب می پردازیم.
معرفی نمودار ضریب بازتاب ساختمان
بر اساس بند 2-3 استاندارد 2800 ویرایش چهارم، ضریب بازتاب ساختمان بیانگر نحوه ی پاسخ ساختمان به حرکت زمین با توجه به نوع آن است. این ضریب با استفاده از رابطه ی زیر به دست می آید:
B=B1N
در رابطه ی فوق B1 برابر با ضریب شکل طیف و N ضریب اصلاح طیف می باشد. ضریب شکل طیف B1، با در نظر گرفتن بزرگنمایی خاک در پریودهای مختلف و میزان لرزه خیزی منطقه مشخص می شود. این ضریب با استفاده از روابط زیر تعیین می گردد:
در این روابط:
T: زمان تناوب اصلی نوسان ساختمان به ثانیه است.
T0 Ts Sو S0: پارامترهایی هستند که به نوع زمین و میزان خطر لرزه خیزی منطقه وابسته اند.
در مثال ساختمان بتنی هفت طبقه، در صورتی که خاک تیپ III باشد و ساختمان در شهر اصفهان (پهنه با خطر نسبی متوسط) قرار گرفته باشد، S برابر با 1.75، S0 برابر با 1.1، T0 برابر با 0.15 و Ts برابر با 0.7 میباشد. بر اساس بند 2-3-2 استاندارد 2800 ویرایش چهارم، ضریب اصلاح N1 به شرح زیر تعیین میشود:
در نهایت با ساده سازی های انجام شده رابطه ضریب بازتاب برای سازه ی مورد نظر به صورت زیر به دست می آید:
جهت ساخت منحنی ضریب بازتاب می توان از برنامه ی اکسل (Excel) استفاده نمود. بدین صورت که ستون اول مربوط به زمان تناوب T و ستون دوم مربوط به مقادیر ضریب بازتاب باشد. در ستون اول مقادیر زمان تناوب را از 0 تا 5 ثانیه و با گام های 0.05 ثانیه وارد می کنیم. سپس مقادیر ضریب بازتاب را بر اساس روابط ارائه شده در قسمت بالا، با استفاده از قابلیت فرمول نویسی برنامه اکسل، در ستون دوم وارد می کنیم. به عنوان مثال برای زمان تناوب 0.75 ثانیه مقدار ضریب بازتاب به صورت شکل زیر در اکسل وارد شده است.
در نهایت جدولی به صورت جدول نشان داده در شکل زیر به دست می آید.
پس اتمام کار در محیط اکسل فایل مورد نظر را به صورت فایل Text در محل فایل ایتبس ذخیره می کنیم.با باز شدن پنجره ی نشان داده شده در شکل (9) روی گزینه ی Yes کلیک میکنیم.

به محیط نرم افزار ایتبس بازگشته و از مسیر زیر وارد پنجره ی نشان داده شده در شکل (9) میشویم و نمودار مربوط به ضریب بازتاب را در نرم افزار فراخوانی میکنیم.
Define > Functions > Response Spectrum
در قسمت Choose Function Type to Add الگوی ضریب بازتاب بر اساس تعدادی از آیین نامه های دنیا وجود دارد. در اینجا با انتخاب گزینه ی From File میتوان الگوی ضریب بازتابی را که در قسمت قبل ساخته بودیم در ایتبس وارد کنیم. از این رو با انتخاب گزینه ی Add New Function پنجره ی نشان داده در شکل (11) ظاهر می شود.

شکل (11): نمودار ضریب بازتاب در نرم افزار ایتبس 2015
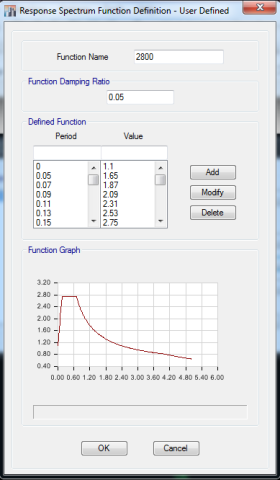
در قسمت مربوط به Function Name نامی دلخواه برای نمودار ضریب بازتاب مورد نظر انتخاب میکنیم. در قسمت مربوط به Function Damping Ratio نسبت میرایی سازه را وارد میکنیم. بر اساس بند 2-5-1 ویرایش چهارم استاندارد 2800 در تعیین طیف طرح استاندارد نسبت میرایی برابر با 5 درصد در نظر گرفته شده است.

با توجه به اینکه ضریب بازتاب بر اساس زمان تناوب تعیین شده است، گزینه ی Period vs Value را انتخاب می کنیم. سپس برای وارد کردن فایل متنی ساخته شده گزینه ی Browse را انتخاب میکنیم و فایل متنی مورد نظر را از مسیر مورد نظر انتخاب می کنیم دقت شود جهت نمایش فایل متنی در قسمت پایین پنجره نوع فایل را Text Files انتخاب کنیم. با انتخاب فایل متنی نمودار ضریب بازتاب مربوطه در پنجره نمایش داده می شود.
با انتخاب گزینه ی View File فایل متنی وارد شده مانند شکل (12) نمایش داده می شود. دقت شود ردیف اول این فایل، عناوین Period و B آورده شده است. بنابر این باید عناوین ذکر شده را از این قسمت حذف کرده و یا در قسمت Header Line to Skip مقدار یک را وارد کرده تا در نمودار، سطر ابتدایی فایل متنی حذف شود.

شکل (12): نمایش اطلاعات فایل متنی ضریب بازتاب در نرم افزار ایتبس
پس از وارد کردن فایل متنی با انتخاب گزینه Convert to User Defined پنجره ی نشان داده شده در شکل (13) نمایش داده می شود. با این کار ایتبس اطلاعات فایل متنی را در فایل مدل ذخیره می کند، در غیر این صورت با باز شدن فایل بر روی سایر سیستمها دوباره باید فایل متنی در مدل وارد شود.
شکل (13): ذخیره و ثبت اطلاعات فایل متنی در مدل ایتبس
با انتخاب گزینه ی OK نمودار مربوط به ضریب بازتاب تعریف شده ذخیره می گردد.
تعریف حالات مختلف بار تحلیل طیفی
جهت تعریف حالات مختلف بار طیفی در نرم افزار ایتبس 2015 از مسیر زیر وارد پنجره ی نشان داده در شکل (14) می شویم.
Define> Load Case> Add New Cases
در قسمت Load Case Name نام حالت بار مورد نظر ( در اینجا به عنوان مثال SX) را وارد می کنیم. در قسمت Load Case Type، گزینه ی Response spectrum را انتخاب می کنیم. سپس در قسمت Load Applied گزینه ی Add را انتخاب می کنیم. از آنجایی که در تحلیل طیفی بار از نوع شتاب می باشد، در قسمت Load Type گزینه ی Acceleration که پیش فرض خود نرم افزار ایتبس می باشد را انتخاب می کنیم. در قسمت Load Name، جهت اعمال بار مشخص می گردد. پارامترهای U1، U2 و U3 به ترتیب بیانگر نیرو در راستای X، Y و Z می باشد. در قسمت Function نمودار ضریب بازتاب تعریف شده در مرحله ی قبل را انتخاب می کنیم. به عنوان مثال در اینجا نموار ضریب بازتاب که با نام 2800 ذخیره شده است انتخاب میکنیم. در Scale Factor ضریب را وارد می کنیم.
به عنوان مثال در سازه ی بتنی مسکونی مثال ارائه شده در این مقاله، مقدار Scale Factor برابر است با:
![]()
از آنجایی که در مثال فوق سیستم سازه ای در هر دو راستا یکسان است، بنابر این مقدارScale Factor برای تمامی حالات بار طیفی یکسان است.
در قسمت Modal Combonation Method روشهای مختلفی جهت ترکیب آثار مودها وجود دارد.
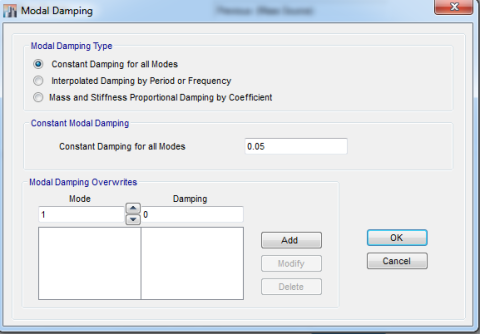
در قسمت Modal Damping نسبت میرایی سازه به نرم افزار ایتبس معرفی می شود. این مقدار بر اساس استاندارد 2800 ویرایش چهارم برابر با 05/0 می باشد که به طور پیش فرض در نرم افزار نیز همین مقدار می باشد.
در قسمت Modal Combination روشهای مختلفی برای ترکیب آثار مودها وجود دارد. در این قسمت گزینه ی CQC را فعال می کنیم. دلیل این انتخاب آن است که بر اساس ویرایش چهارم استاندارد 2800 در استفاده از این روش محدودیتی وجود ندارد؛ در حالی که استفاده از این روش در ساختمان های نامنظم در پلان و ساختمان هایی که پیچش در آنها حائز اهمیت می باشد، استفاده از این روش به عنوان تنها روش قابل استفاده مطرح میباشد.
در قسمت Directional Combination روشهای مختلفی جهت ترکیب نتایج طیفها وجود دارد. در این قسمت گزینه ی پیش فرض برنامه یعنی روش ترکیب SRSS روش مناسبی میباشد.
با کلیک بر روی Modify در قسمت Modal Damping Type وارد پنجرهی نشان داده شده در شکل (15) میشویم.
در این قسمت تنظیمات پیش فرض (انتخاب گزینه ی Constant Damping for all Modes و وارد نمودن عدد 05/0 جهت نسبت میرایی) مناسب میباشد. در قسمت Modal Damping Overwrites میتوان به هر مود به طور مجزا مقدار میرایی دلخواهی اختصاص داد.
قسمت Diaphragm Eccentricity نشان داده شده در شکل (14)، مربوط به برون محوری اتفاقی میباشد؛ که در تعریف SX و SY این مقدار برابر با صفر میباشد.
پس از تعریف حالت بار SX به همین صورت سایر حالتهای بارگذاری را تعریف میکنیم. به عنوان مثال با انتخاب گزینه ی Add Copy of Case… از حالت بارگذاری SX کپی تهیه نموده و نام آن را به SY تغییر میدهیم. در این حالت با تغییر U1 به U2 و انتخاب نمودار ضریب بازتاب و Scale Factor مربوط به راستای مورد نظر (در مثال فوق به علت یکسان بودن سیستم سازه ای در دو جهت موارد فوق یکسان میباشد) و تغییر نام حالت بارگذاری به SY، حالت بارگذاری مورد نظر ساخته میشود.

شکل (14): تعریف حالات بارگذاری دینامیکی
شکل (15): نسبت میرایی حالات بارگذاری دینامیکی
حالتهای بارگذاری SXPN و SYPN به ترتیب مشابه حالات بار SX و SY می باشند؛ با این تفاوت که مقدار Eccentricity Ratio در قسمت Diaphragm Eccentricity برای هر دو حالت بارگذاری برابر با 0/05 می باشد. باید توجه داشت که در صورتی که سازه دارای نامنظمی پیچشی باشد، مقدار خروج از مرکزیت برای هر طبقه به صورت مجزا در قسمت Overwrites at Specific Diaphragms تعریف میشود.
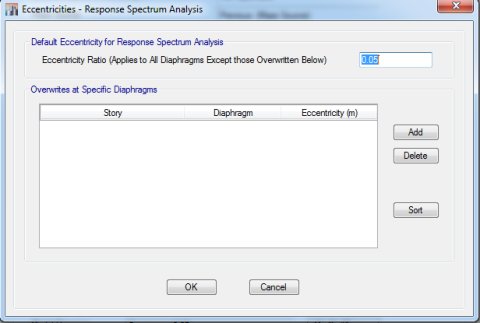
شکل (16): خروج از مرکزیت اتفاقی حالات بارگذاری دینامیکی
در صورت وجود نامنظمی پیچشی (در پلانهای نامنظم که نسبت تغييرمکان ماکزیمم به تعييرمکان متوسط بزرگتر از 1.2 میباشد) باید اثرات پیچش تصادفی در نظر گرفته شود. در ادامه به چگونگی محاسبه ی پیچش تصادفی و تعیین ضریب Aj در سازه های نامنظم خواهیم پرداخت.
پیچش تصادفی و محاسبه ی ضریب Aj
بر اساس بند 3-3-7-3 ویرایش چهارم استاندارد 2800 برون مرکزی اتفاقی در تراز طبقه، به منظور به حساب آوردن احتمال تغییرات اتفاقی توزیع جرم و سختی از یک سو و نیروی ناشی از مؤلفه ی پیچشی زلزله از سوی دیگر، در نظرگرفته میشود. این برون مرکزی باید در دو جهت و حداقل برابر با 50 درصد بعد ساختمان در آن طبقه در امتداد عمود بر نیروی جانبی اختیار شود. در مواردی که ساختمان مشمول نامنظمی پیچشی میشود، برون مرکزی اتفاقی حداقل باید در ضریب بزرگنمایی Aj، طبق رابطه ی زیر ضرب شود.
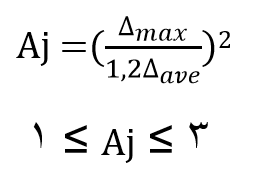
در این رابطه:
maxΔ = حداکثر تغییر مکان طبقه j، که با فرض Aj = 1 محاسبه شده است.
aveΔ = میانگین تغییر مکان دو انتهای ساختمان در طبقه j، که با فرض Aj = 1 محاسبه شده است.
بر اساس زلزله ی استاتیکی در سازه مقدار خروج از مرکزیت به شرح زیر به دست میآید:
Aj×0.05×L = خروج از مرکزیت
L = بعد ساختمان در طبقه ی مورد نظر در امتداد عمود بر نیروی جانبی

بر اساس بند 3-3-7-4 ویرایش چهارم استاندارد 2800 در ساختمان های تا پنج طبقه و یا کوتاهتر از هجده متر در مواردی که برون مرکزی نیروی جانبی طبقه در طبقات بالاتر از هر طبقه کمتر از 5 درصد بعد ساختمان در آن طبقه در امتداد عمود بر نیروی جانبی باشد، برای محاسبات لنگر پیچشی نیازی به در نظر گرفتن برون مرکزی اتفاقی در طبقات نیست. بنابر این در شرایط خاص ذکر شده در بند فوق میتوان از خروج از مرکزیت اتفاقی صرف نظر نمود.

جهت تعیین مقدار ضریب بزرگنمایی Aj میتوان به شرح زیر عمل کرد:
همانگونه که در قسمت بالا اشاره شد مقدار ضریب بزرگنمایی Aj برابر است با:

جهت محاسبه ی مقدار در نرم افزار ایتبس ابتدا سازه را آنالیز کرده و سپس از مسیر زیر وارد پنجره ی نشان داده شده در شکل (19) میشویم.
Diplay > Show Tables > Analysis > Results > Displacements > Diaphragm Max/Avg Drifts
در قسمت Load Case/ Combo، زلزله های دارای خروج از مرکزیت0/05 را انتخاب کرده و در قسمت Item راستای X را انتخاب میکنیم.
شکل (19): محاسبه ی مقدار با مقدار در نرم افزار ایتبس جهت محاسبه ی ضریب بزرگنمایی

شکل (19): محاسبه ی مقدار با مقدار در نرم افزار ایتبس جهت محاسبه ی ضریب بزرگنمایی
ستون مربوط به Ratio در این جدول برابر با مقدار میباشد. ستون مربوط به Ratio را در برنامه ی اکسل کپی میکنیم و مقدار Aj را در ستون مقابل، با تقسیم مقدار Ratio بر 1.2 و به توان 2 رساندن مقدار به دست آمده محاسبه میکنیم. پس از محاسبه ی مقدار ضریب بزرگنمایی Aj، مقدار خروج از مرکزیت در طبقاتی که مقدار Aj در آنها بیشتر از 1 میباشد باید اصلاح گردد. به عنوان مثال، با توجه به شکل (21)، در سازهی ارائه شده در این مقاله مقدار ضریب بزرگ نمایی مربوط به طبقات 1، 3، 4، 5 و 6 بیشتر از یک میباشد؛ و مقدار خروج از مرکزیت در این طبقات بیشتر از 0.05 می باشد. بنابراین در ستون چهارم از شکل (21) مقدارخروج از مرکزیت اتفاقی را به صورت زیر به دست می آوریم :
Aj×0.05×L=خروج از مرکزیت
با توجه به شکل زیر برای زلزله ی راستای X، مقدار بعد در راستای عمود بر نیروی زلزله برابر با19 متر میباشد.
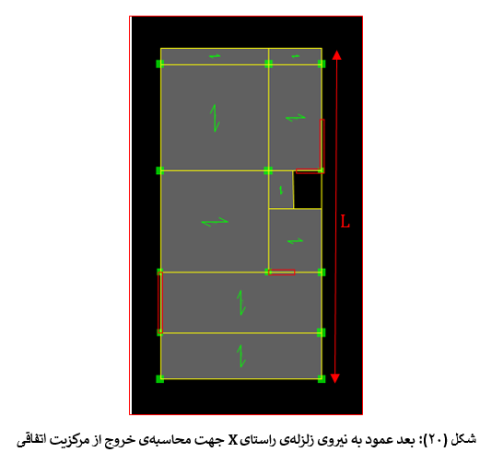
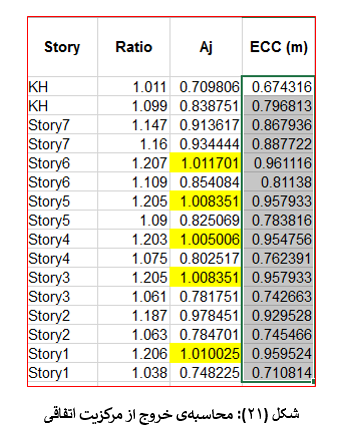
جهت وارد کردن مقادیر خروج از مرکزیت های به دست آمده در طبقات، در نرم افزار ایتبس 2015 به صورت زیر عمل میکنیم:
Define> Load Case> SXPN > Modify/ Show Case…
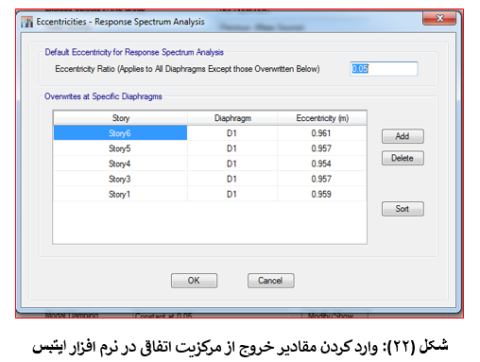
در قسمت Diaphragm Eccentricity گزینه ی Modify را انتخاب کرده و وارد پنجره ی نشان داده شده در شکل (22) میشویم. در قسمت Overwrites at Specific Diaphragms با انتخاب گزینه ی Add ردیف جدیدی جهت وارد کردن اطلاعات مربوط به طبقات دارای خروج از مرکزیت بیشتر از 0.05 ایجاد میگردد.
در قسمت Story، طبقه ی مورد نظر و در قسمت Eccentricity مقدار خروج از مرکزیت محاسبه شده در قسمت بالا را مطابق شکل (22) وارد میکنیم.
ترکیب بارهای طراحی در حالت تحلیل دینامیکی طیفی
مطابق بند 5-3-1 از استاندارد ACI318 ویرایش 2019، در طراحی ساختمان های بتنی، ترکیبات بارگذاری زیر مورد استفاده قرار میگیرند.
1) U= 1.4 D
2) U= 1.2D+ 1.6 L+ 0.5(Lr or S or R)
3) U= 1.2D+ ( L or 0.5 W)+ 1.6(Lr or S or R)
4) U= 1.2D+ L+ W+ 0.5(Lr or S or R)
5) U= 1.2 D+ L+ W+ 0.2S+E
6) U= 0.9D+ W
7) U= 0.9D+ E
نکته ای که در ارتباط با ترکیب بارها باید به آن توجه نمود این است که بر اساس بند 3-3-9 ویرایش چهارم استاندارد 2800، نیروی قائم ناشی از زلزله که اثر مؤلفه قائم شتاب زلزله در ساختمان است، در موارد زیر باید در محاسبات منظور شود.
الف) کل سازه ساختمان هایی که در پهنه با خطر نسبی خیلی زیاد واقع شده اند.
ب) تیرهایی که دهانه آنها بیشتر از پانزده متر میباشد، همراه با ستونها و دیوارهای تکیه گاهی آنها.
پ) تیرهایی که بار قائم متمرکز قابل توجهی در مقایسه با سایر بارهای منتقل شده به تیر را تحمل میکنند، همراه با ستونها و دیوارهای تکیه گاهی آنها. در صورتی که بار متمرکز حداقل برابر با نصف مجموع بار وارده به تیر باشد، آن بار قابل توجه تلقی میشود.
بر اساس این بند مقدار این نیروی قائم از رابطه ی زیر به دست می آید:
Fv = 0.6 AIWp
در این رابطه:
A و I مقادیری هستند که برای محاسبه ی نیروی برشی پایه منظور شده اند.
Wp: در مورد بند الف بالا بار مرده و در مورد سایر بندها بار مرده به اضافه کل سربار است.
نیروی قائم زلزله باید در هر دو جهت رو به بالا و رو به پایین، جداگانه به سازه اعمال شود. در نظر گرفتن نیروی قائم در جهت رو به بالا در طراحی پی ساختمان ضروری نیست. بر اساس بند 3-3-9-3 از همین استاندارد، نیروهای قائم و افقی زلزله باید همزمان با بارهای مرده و زنده ترکیب شده و در طراحی اعضای سازه به کار رود. سازه باید برای بیشینه اثر این ترکیبات طراحی گردد.
در سازه هایی با ضریب اهمیت I=1 که در پهنه با خطر نسبی خیلی زیاد قرار گرفته اند، باید مؤلفه ی قائم زلزله در دو جهت مثبت و منفی (یعنی جهات رو به بالا و رو به پایین) به کل سازه اعمال شود. بنابر این ترکیبات بارگذاری در این سازه ها را میتوان به صورت زیر اصلاح نمود.

از بین دو ترکیب بار 5-1 و 5-2 ترکیب بار 5-1 با مقدار ضریب بار مرده ی بیشتر بحرانی تر میباشد؛ و از آنجایی که دو ترکیب 7-1 و 7-2 معمولاً برای کنترل آپلیفت مورد استفاده قرار میگیرند، ترکیب 7-2 با ضریب بار مرده ی کمتر بحرانی تر میباشد. بنابراین نیازی به ساخت دو ترکیب بار اضافی دیگر نیست.
بر اساس بند 3-1-4 ویرایش چهارم استاندارد 2800، ساختمان باید در دو امتداد عمود بر هم در برابر نیروی زلزله محاسبه شود. به طور کلی میتوان محاسبه در هر یک از این دو امتداد را جز در موارد زیر به طور مجزا و بدون در نظر گرفتن نیروی زلزله در امتداد دیگر انجام داد.
الف) ساختمان های نامنظم در پلان
ب) کلیه ستون هایی که در محل تقاطع دو و یا چند سیستم مقاوم باربر جانبی قرار دارند. در این مورد چنانچه بار محوری ناشی از زلزله در ستون، در هر یک از دو امتداد مورد نظر کمتر از 20 درصد ظرفیت بار محوری ستون باشد، این ضابطه را میتوان نادیده گرفت.
در موارد فوق امتداد نیروی زلزله باید با زاویه مناسبی که حتی المقدور بیشترین اثر را ایجاد میکند، انتخاب شود و یا میتوان صد در صد نیروی زلزله هر امتداد را با 30 درصد نیروی زلزله در امتداد عمود بر آن ترکیب کرد. در این موارد منظور کردن برون مرکزی اتفاقی، در امتدادی که 30 درصد نیرو اعمال میشود، الزامی نیست.
در تحلیل طیفی پس از تعریف حالات بارگذای SX، SY، SXPN، SYPN که در قسمتهای قبل به شرح آن پرداخته شده است، حالات بارگذاری فوق به صورت زیر با یکدیگر ترکیب میشوند. باید در نظر داشت که در تحلیل دینامیکی طیفی نیازی نیست که بار زلزله در دو جهت رفت و برگشتی (مثبت و منفی) به سازه اعمال شود. در واقع در این حالت، نرم افزار ایتبس به صورت خودکار بار زلزله را در دو جهت اعمال میکند و مقدار حداکثر پاسخها را برای طراحی در نظر میگیرد. این قابلیت ایتبس باعث میشود تعداد ترکیب بارها در ایتبس به تعداد قابل توجهی کاهش پیدا کند.
بر اساس بند 3-3-2 ویرایش چهارم استاندارد 2800، ساختمان هایی که سیستم مقاوم جانبی آنها در دو جهت عمود بر هم دارای نامعینی کافی نیستند، باید برای بار جانبی بیشتری طراحی شوند. در این ساختمانها بار جانبی باید با ضریب نامعینی سازه (ρ برابر با 1.2) افزایش داده شود. بر اساس بند 3-3-2-2 همین استاندارد ساختمان هایی که سیستم مقاوم جانبی آنها دارای خصوصیات زیر هستند، دارای نامعینی کافی بوده و در آنها ضریب ρ برابر با 1 منظور میشود.
الف) در ساختمان های منظم در پلان، در طبقاتی که برش در آنها از 35 درصد برش پایه تجاوز میکند، حداقل دو دهانه سیستم مقاوم جانبی در هر سمت مرکز جرم، در هر دو امتداد عمود بر هم موجود باشد. در سیستمهای دارای دیوار برشی تعداد دهانه ها از تقسیم طول دیوار بر ارتفاع آن در طبقه به دست می آید.
ب) در سایر ساختمانها، در طبقاتی که میزان برش در آنها از 35 درصد برش پایه تجاوز میکند، چنانچه حذف جزئی از سیستم مقاوم جانبی، موجب کاهش مقاومت جانبی طبقه به میزان 33 درصد نشود و در طبقه نامنظمی شدید پیچشی ایجاد نگردد.
بنابر این، با توجه به مطالب ارائه شده، کلیه ی ترکیب بارهای بحرانی، به صورت ساده شده، در حالت طیفی دینامیکی و با در نظرگیری اثر ترکیب بارهای صد- سی و ضریب نامعینی سازه به شرح زیر میباشد.
از آنجایی که ممکن است مقدار ضریب نامعینی در دو راستای X و Y متفاوت باشند از دو پارامتر xρ و yρ جهت معرفی ضریب نامعینی استفاده شده است.
1) U= 1.4 D
2) U= 1.2D+ 1.6 L+ 0.5(Lr or S)
3) U= 1.2D+ L+ 1.6(Lr or S)
4-1) U= 1.41D+ L+ 0.2S+ ρx SXPN+ 0.3 ρy SY
4-2) U= 1.41D+ L+ 0.2S+ ρy SYPN+ 0.3 ρx SX
5-1) U= 0.69 D+ ρx SXPN+0.3 ρy SY
5-2) U= 0.69 D+ ρy SYPN+0.3 ρx SX
همان طور که قبلاً نیز اشاره شد تعداد ترکیب بارهای حالت دینامیکی طیفی نسبت به حالت استاتیکی طیفی به شدت کمتر میباشد.
جهت تعریف ترکیب بارهای ذکر شده در نرم افزار ایتبس از مسیر زیر اقدام میکنیم.
Define > Load Combination > Add New Combo…
پیشنهاد آموزشی : آموزش پروژه محور طراحی سازه فولادی و بتنی با ایتبس و سیف (اینجا کلیک کنید)
هم پایه کردن برش پایه تحلیل دینامیکی طیفی با برش پایه تحلیل استاتیکی
پس از تحلیل اولیه سازه، زلزله های دینامیکی باید با زلزله استاتیکی همپایه شوند. بر اساس بند 3-4-1-4 ویرایش چهارم استاندارد 2800، در مواردی که برش پایه به دست آمده از روش تحلیل طیفی کمتر از برش پایه استاتیکی معادل باشد، مقدار برش پایه تحلیل طیفی باید به مقدار زیر افزایش داده شده و بازتاب های سازه متناسب با آنها اصلاح گردد.
الف) در سازه های نامنظم، که نامنظمی در آنها از نوع طبقه خیلی ضعیف یا طبقه خیلی نرم یا پیچشی شدید نباشد، مقدار بازتابها باید در 90 درصد نسبت برش پایه استاتیکی معادل به برش پایه به دست آمده از تحلیل طیفی ضرب شوند. ولی در سازه های نامنظمی که نامنظمی در آنها مشمول موارد فوق الذکر باشد، مقادیر بازتابها باید در نسبت برش پایه استاتیکی معادل به برش به دست آمده از تحلیل طیفی ضرب شود.
ب) در سازه های منظم، مقادیر بازتابها باید در 85 درصد نسبت برش پایه استاتیکی معادل به برش پایه به دست آمده از تحلیل طیفی ضرب شود.
بنابر این ضریب همپایگی برش پایه به نوع نامنظمی سازه وابسته است. بنابر این در ابتدا باید نوع نامنظمی های احتمالی سازه تعیین گردد.
باید توجه داشت که مقادیر برش پایه ی تعدیل شده در بندهای الف و ب نباید از برش پایه به دست آمده از تحلیل استاتیکی کمتر در نظر گرفته شود. در حقیقت اگر برش پایه دینامیکی از برش پایه استاتیکی بیشتر شود و ضریب همپایگی کمتر از یک شود نیازی به همپایه سازی وجود ندارد و ضریب اصلاح برابر یک میباشد. در قابهای خمشی معمولاً برش پایه استاتیکی بیشتر از برش پایه دینامیکی میباشد؛ مگر آنکه در طراحی از تیر و ستونهای با سختی زیاد استفاده شده باشد. همچنین در مواردی که از دیوار برشی و یا بادبند با سختی زیاد استفاده شود نیز ممکن است برش پایه دینامیکی بیشتر از برش پایه استاتیکی شود.
به عنوان مثال در سازه ی ارائه شده در این مقاله نامنظمی از نوع طبقه ی خیلی ضعیف یا خیلی نرم یا پیچشی شدید نمیباشد، در این حالت زلزله ی دینامیکی با 90 درصد زلزله ی استاتیکی همپایه میگردد. بنابر این ضریب همپایگی به صورت زیر محاسبه میشود:
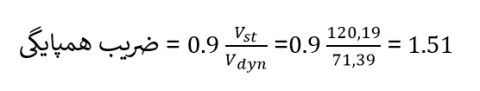
چگونگی محاسبه ی ضریب همپایگی در نرم افزار ایتبس 2015 به شرح زیر میباشد.
پس از آنالیز سازه از مسیر زیر وارد پنچره ی نشان داده شده در شکل (23) میشویم.
Diplay > Show Tables > Analysis > Results > Reactions > Base Reactions

شکل (23): مقادیر برش پایه ی استاتیکی و دینامیکی در نرم افزار ایتبس
در قسمت Load Case/ Combo، زلزله ی استاتیکی EXP و EXN و زلزله های
دینامیکی SX و SXPN را انتخاب میکنیم. با توجه به شکل (23) مقدار برش پایه استاتیکی در راستای X به برش پایه دینامیکی در راستای X به صورت زیر میباشد.
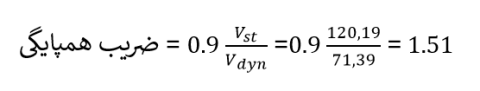
جهت اعمال ضریب همپایگی از مسیر زیر وارد پنجره ی نشان داده شده در شکل (24) میشویم.
Define> Load Case> SX و SXPN انتخاب > Modify Show Cases
در پنجره ی نشان داده شده در شکل (24)، در قسمتScale Factor مقدار AIg/R را در مقدار ضریب همپایگی ضرب میکنیم.
عمل همپایگی برش پایه دینامیکی را برای راستای Y نیز به همین صورت انجام میدهیم.
با توجه به شکل (23) متوجه میشویم که برش پایه استاتیکی تنها در راستای اعمال نیروی زلزله ی استاتیکی میباشد؛ اما این موضوع در مورد زلزله ی دینامیکی صادق نیست.
هم پایه سازی در این حالت به دو صورت انجام میشود:
- بر اساس مؤلفه
در این حالت همانند مثال بالا تنها مقدار برش پایه دینامیکی در راستای مورد نظر در همپایه سازی مورد استفاده قرار میگیرد.
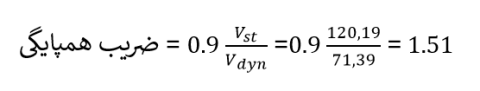
- بر اساس برآیند برداری
در این حالت برآیند برداری برش پایه دینامیکی در دو راستا در نظر گرفته میشود. به عنوان مثال ضریب همپایگی برای مورد ارائه شده در بالا به شرح زیر میباشد.
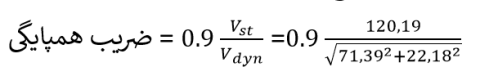
بسیاری از مهندسان از روش دوم جهت همپایه سازی برش پایه دینامیکی استفاده میکنند؛ اما باید توجه نمود که مؤلفه های مربوط به زلزله دینامیکی خاصیت برداری ندارند و اصولاً محاسبه برآیند برداری آنها صحیح نیست. در سازه های نامنظم تفاوت دو روش ذکر شده میتواند زیاد باشد. با توجه به اینکه در روش اول برش پایه ی دینامیکی مقدار کمتری نسبت به برش پایه ی دینامیکی در روش دوم دارد، در نتیجه مقدار ضریب همپایگی روش اول بیشتر بوده و استفاده از روش اول در جهت اطمینان میباشد. باید توجه داشت که محاسبه برآیند برداری برای زلزله دینامیکی یک روش غیر علمی میباشد که در بین مهندسین رایج شده است.
شکل (24): همپایه سازی برش پایه دینامیکی در نرم افزار ایتبس

شکل (24): همپایه سازی برش پایه دینامیکی در نرم افزار ایتبس
کنترلهای مورد نیاز آنالیز دینامیکی
کنترل تعداد مودهای نوسان
با توجه به بند 3-4-1-2 ویرایش چهارم استاندارد 2800 و بند 12-9-1 استاندارد ASCE-7-22، در هر یک از دو امتداد متعامد نوسان باید تعداد مودهای نوسان که مجموع جرمهای مؤثر در آنها بیش از 90 درصد جرم کل سازه است، در نظر گرفته شود.

شکل (25): بند 3-4-1-2 ویرایش چهارم استاندارد 2800

شکل (26): بند 12-9-1 استاندارد ASCE-7-22
جهت کنترل این بند از ویرایش چهارم استاندارد 2800، پس از آنالیز سازه از مسیر زیر وارد پنجره ی نشان داده شده در شکل (27) میشویم.
Diplay > Show Tables > Analysis > Results > Modal Results > Modal Participating Mass Ratios
با توجه به شکل (27)، برای اینکه در هر دو جهت ۹۰ درصد جرم موثر منظور شود باید حداقل 17 مد انتخاب شود.
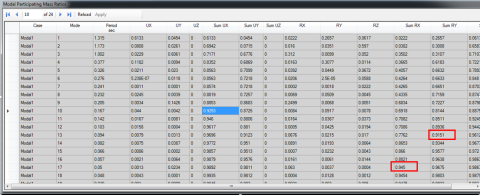
شکل (27): کنترل مجموع جرم مؤثر در تحلیل دینامیکی
کنترل دریفت تحت زلزله ی دینامیکی طیفی
جهت کنترل دریفت سازه در نرم افزار ایتبس2016 ، ابتدا از فایل اصلی Save As تهیه کرده. سپس در فایل مورد نظر مقادیر ضرایب ترک خوردگی تیرها را 0.5 و ستونها و دیوارها را 1 وارد میکنیم. سپس سازه را تحلیل کرده و از مسیر زیر وارد پنجره ی نشان داده شده در شکل (28) میشویم.
Diplay > Show Tables > Analysis > Results > Modal Results > Modal Participating Mass Ratios

شکل (28): به دست آوردن زمان تناوب تحلیلی سازه
زمان تناوب مودی از سازه که دارای بیشترین درصد مشارکت جرمی در راستای X و Y میباشد را انتخاب میکنیم. با توجه به زمان تناوب های تحلیلی به دست آمده ضریب زلزله ی استاتیکی سازه را به دست می آوریم.
از منوی Define قسمت Load Pattern زلزله های استاتیکی EXDrift و EYDrift را مطابق شکل (29) تعریف میکنیم و ضریب زلزله ی به دست آمده در مرحله قبل را در EXDrift و EYDrift وارد میکنیم.
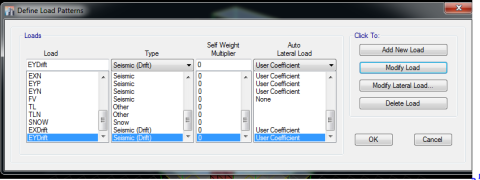
شکل (29): تعریف حالت های بارگذاری EXDrift و EYDrift در نرم افزار ایتبس
سپس از منوی Define قسمت Load Cases زلزله ی دینامیکی دریفت را همانند زلزله های دینامیکی SY و SX تعریف کرده. در قسمت Scale Factor مربوط به زلزله ی دینامیکی دریفت، مقدار Scale اولیه، یعنی AIg/R را همان گونه که در شکل (30) نشان داده شده، وارد میکنیم.
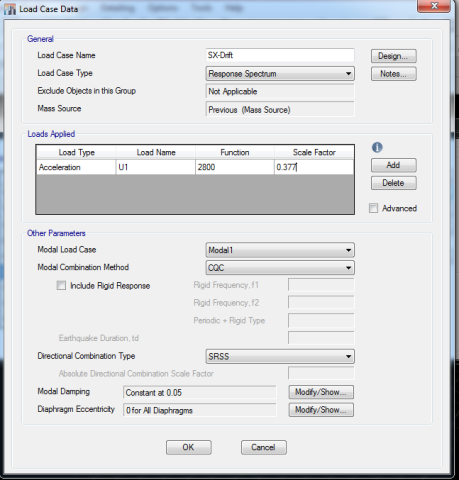
شکل (30): تعریف حالتهای بارگذاری SX-Drift و SY-Drift در نرم افزار ایتبس 2015
سپس همانند آنچه در قسمتهای قبلی ذکر شد، زلزله ی دینامیکی دریفت را با زلزله ی استاتیکی همپایه سازی میکنیم. پس از همپایه کردن زلزله ی دریفت مقدارdrift سازه را تحت بارهای EXDrift و EYDrift از مسیر زیر به دست می آوریم.
Display > Show Tables > Results > Displacements > Diaphragm Max/Ave Drifts
نکته: در هنگام تحلیل دینامیکی طیفی باید توجه نمود با اعمال هر گونه تغییر در مقاطع اعضا و به عبارتی تغییر سختی سازه عمل همپایه سازی باید مجدداً انجام شود.
منابع :
- آیین نامه طراحی ساختمانها در برابر زلزله استاندارد 2800 (ویرایش 4)
- مبحث نهم مقررات ملی ساختمان، ویرایش 1399
- استاندارد بارگذاری آمریکا (ASCE7-22)
- پک پاراسیویل مهندس امیرطه نوروزی
- جزوه طراحی سازه های بتنی و فولادی نوشته ی دکتر حسین زاده اصل