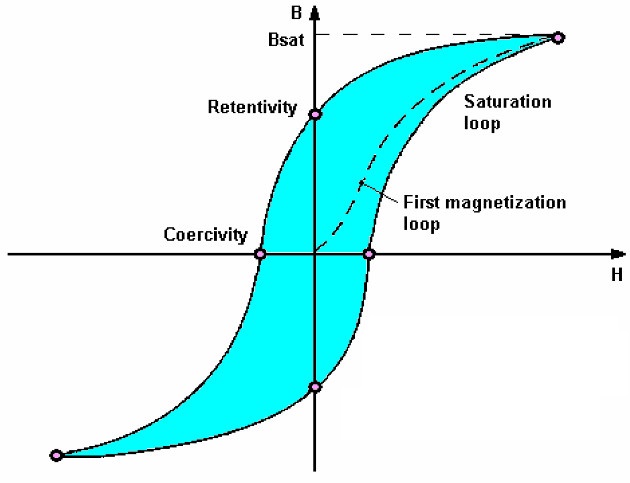
با توجه به لزوم استفاده از تحلیل های غیرخطی به ویژه حالت دینامیکی آن، برای کاربردهایی مثل ارزیابی لرزهای سازه ها نیاز به شناخت رفتار سازه و یا المان در ناحیه ی غیر خطی داریم. از طرف دیگر سازه ها در بارگذاری های سیکلی (رفت و برگشتی مثل نیروی زلزله) رفتار متفاوتی از خود نشان میدهند، لذا لازم است که رفتار سازه در بارهای سیکلی و همچنین میزان انرژی مستهلک شده در جریان این سیکل ها را به خوبی درک کنیم. به عبارت دیگر منحنی هیسترزیس برای بررسی رفتار مصالح تحت بار رفت و برگشتی در زمان وقوع زمینلرزه بکار گرفته میشود. لذا در این مقاله سعی شده است منحنی هیسترزیس و لزوم استفاده از آن توضیح داده شود و رفتارهای آن شناسایی گردد.
پیشنهاد مطالعاتی:
مقاله انواع روش های خطی و غیر خطی تحلیل سازه
تعاریف
هیسترزیس به معنای مسیر رفتار یک سیستم نسبت به حالت قبلی خود است. در مهندسی سازه منحنی هیسترزیس، منحنی بار-تغییرشکل سیستم تحت بارهای متناوب میباشد. اصطلاح هیسترزیس برگرفته از زبان یونانی به معنی کم آوردن و یا عقب ماندن ناشی از حرکت آهسته میباشد. این اصطلاح برای اولین بار در سال 1980 میلادی توسط جیمز آلفرد اوینگ (James Alfred Ewing) جهت توصیف رفتار مواد مغناطیسی استفاده شد.
پدیده هیسترزیس در سیستم های مهندسی تاریخچهای دیرینه داشته و برای مدت طولانی توجه بسیاری از محققین را به خود جلب کرده است. میتوان ادعا کرد که هیسترزیس در همه جا وجود دارد و به همین علت در بسیاری از زمینه های مختلف علم با آن رو به رو می شویم. درک پدیده هیسترزیس و مکانیسم رفتار هیسترتیک در طراحی و تحلیل انواع متعددی از سیستم های مهندسی اهمیت بالایی دارد. رفتار هیسترتیک را در مطالعه میدانهای مغناطیسی، پاسخ دینامیکی بسیاری از سازهها تحت بارگذاریهای چرخهای یا تصادفی با شدت بالا، در روابط نیرو-جابجایی سیستمهای کنترل ارتعاش و در رفتار پاسخ دینامیکی اتصالات میتوان مشاهده نمود.
این منحنی بیانگر رفتار غیرالاستیک سیستم است و به نوع مصالح بکار رفته و نوع سیستم سازهای وابسته میباشد. همچنین با استفاده از این منحنی می توان اطلاعات مهمی را در مورد ویژگی های دینامیکی سازه، انرژی پذیری و نحوه رفتار سازه حین اعمال نیرو به سازه، بدست آورد.
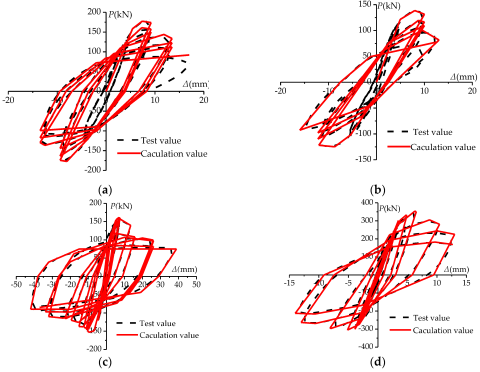
شکل 1 – چند نمونه منحنی هیسترزیس
روشهای تحلیل سازه:
استفاده از تحلیل غیرخطی امروزه به طور گسترده توسط مهندسین سازه به عنوان کمکی برای ارزیابی لرزه ای، انفجار ساختمان ها و سازه های غیرساختمانی استفاده می شود. در اواخر دهه 1990، تحلیل غیرخطی به ندرت توسط مهندسین سازه استفاده می شد، اما به عنوان یک ابزار تحقیقاتی و در موارد استثنا مثل طراحی و ارزیابی سازههای ژاکت فولادی، طراحی سیستم های جداسازی لرزه ای ساختمان ها، طراحی سازه هایی که دارای سیستم های میرایی فعال هستند، استفاده میگردید.
تحلیل غیرخطی سازه، بهسازی لرزهای
طراحی سازه
پس از انتشار آیین نامه های ATC-40 و FEMA 273/274، وضعیت موجود به سرعت دچار تغییر شد. این آیین نامه ها معیارهای طراحی مرتبط با استفاده از تحلیل غیرخطی را ارائه نمودند که میتوانست مستقیماً برای ارزیابی طیف وسیعی از ساختمانهای موجود و طراحی مقاومسازی برای آنها، استفاده شود.
محققین دریافتند که استفاده از تحلیل غیرخطی میتواند سودمند باشد و امکان ارزیابی مطمئنتر عملکرد ساختمان و همچنین طراحی اقتصادیتر را فراهم سازد. دو نوع تحلیل لرزه ای غیرخطی وجود دارد: استاتیکی و دینامیکی، که در ادامه به توضیح آنها پرداخته خواهند شد.
قابل ذکر است که روش دینامیکی غیرخطی برای ارزیابی رفتار دقیق سازه ها تحت زلزله مورد استفاده قرار میگیرد و این در حالیست که روش استاتیکی غیرخطی یا همان روش پوش آور، در ارزیابی آسیبپذیری سازه ها و مطالعات مقاومسازی کاربرد بیشتری دارد.
پیشنهاد مطالعاتی:
مقاله روشهای مقاوم سازی ساختمان در برابر زلزله( راهنمای گام به گام)
تحلیل استاتیکی غیرخطی
تحلیل استاتیکی غیرخطی یا تحلیل پوش آور، تحلیلی است که در آن با توجه به شکل مود اول در هر راستا توسط یک بارگذاری استاتیکی، سازه مد نظر تا زمان رسیدن به یک مقدار جابجایی مشخص که این جابجایی تغییرمکان هدف نام دارد، پوش میشود. یا به عبارت دیگر میتوان گفت که یک نیروی معین به مرکز جرم بام ساختمان وارد شده و سازه بطور آرام و تدریجی جابجا می شود تا زمانی که به یک تغییر مکان معین (تغییر مکان هدف) برسد، سپس نیروی مورد نیاز برای تمام المانها و نیروهای سازه ای در تمام سطوح مربوط به آن بارگذاری ثبت شده و همچنین کل بار اعمال شده به شکل نیروی برشی پایه V ثبت میگردد. این روش تا زمانی تکرار می شود که:
- جابجایی هدف به دست آید.
- ناپایداری ساختاری رخ دهد.
- شکست بحرانی در یک یا چند عنصر سازه پیشبینی شود.
پس از اتمام تجزیه و تحلیل پوش آور، منحنی تحت عنوان منحنی پوش آور رسم میشود. منحنی پوش آور نموداری از کل نیروی برشی جانبی اعمال شده V در هر افزایش بارگذاری، در برابر جابجایی جانبی نسبت به یک محل مرجع است که معمولاً به عنوان مرکز جرم در بالاترین سطح سازه در نظر گرفته می شود.
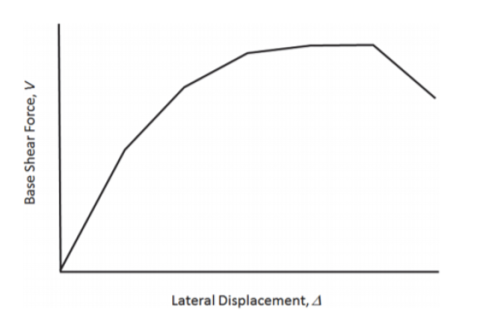
شکل 2- منحنی پوش آور
پارامترهای ورودی مورد نیاز برای انجام یک تحلیل پوش آور عبارتند از: هندسه سازه،اتصالات ،شرایط مرزی و همچنین نمودار رفتار تغییرشکل-نیرو هر المان در طیف وسیعی از تغییر شکل ها.
باید به این نکته توجه نمود که چون تحلیل استاتیکی غیرخطی مستقیماً رفتار دینامیکی و بارگذاری معکوس را شبیهسازی نمیکند، تأثیرات تخریب سیکلی که بسیاری از المانهای سازه ای در معرض تقاضاهای غیرالاستیک سیکلی بزرگ قرار میگیرند، باید از طریق انتخاب روابط بکبون (Backbone relationships) که مقدار فرضی این تخریب را به حساب میآورند، تقریب زده شوند.
در بند 3 از پیوست دوم استاندارد 2800 از تحلیل استاتیکی غیر خطی صحبت شده است:
- تحلیل استاتیکی غیرخطی یک سازه با اعمال بارهای ثقلی ثابت و بارهای جانبی رانشی انجام میشود. اثر نیرو نیز در انجام این تحلیل باید در نظر گرفته شود. از این روش میتوان برای ارزیابی عملکرد سازه در تغییرمکان هدف و نیز محاسبه مقدار ضریب اضافه مقاومت سازه استفاده کرد.
- از روش تحلیل استاتیکی غیرخطی در سازههایی میتوان استفاده نمود که در آنها اثر مودهای بالا عمده نباشد. برای تعیین این موضوع ضروری است سازه ساختمان دو بار با استفاده از روش تحلیل دینامیکی طیفی تحلیل شود. در بار اول تنها مود اول سازه در نظر گرفته شده و در بار دوم تمام مودهای نوسانی که مجموع جرم مؤثر آنها حداقل 90% جرم کل سازه است باید در نظر گرفته شود. در صورتی که نتایج حاصل از تحلیل اول بزرگتر است، این امر به معنی عمده بودن اثر مودهای بالای سازه است.
پیشنهاد مطالعاتی:
مقاله تحلیل دینامیکی طیفی چیست و چگونه در ایتبس انجام می شود؟ به همراه بررسی پروژه واقعی
- در این روش تاثیر زلزله باید در هر دو جهت مثبت و منفی در هر امتداد اصلی به ساختمان اعمال گردد و بحرانیترین مقادیر تلاشها و تغییرشکلهای ایجاد شده ملاک طراحی و کنترل اعضا قرار گیرد.
- در مورد ساختمانهای منظم میتوان تحلیل را در هر امتداد اصلی افقی بطور مستقل انجام داد.
- در مورد ساختمانهای نامنظم باید از مدلهای سهبعدی در تحلیل استفاده کرد. آثار دو مؤلفه افقی زلزله نیز باید محلوظ گردد. برای در نظر گرفتن این آثار در مورد این ساختمانها و نیز آن دسته از ساختمانهای منظم که دارای یک یا چند ستون مشترک بین دو یا چند قاب سیستم باربر جانبی در جهات مختلف باشد، در تحلیل استاتیکی غیرخطی باید در هر امتداد 100% نیروها و تغییرمکانها در جهت مورد بررسی به همراه نیروهای متناظر با 30% تغییرمکان در امتداد عمود بر آن در نظر گرفته شود.
- حداقل دو توزیع بار جانبی به شرح زیر باید در تحلیل اعمال گردد :
الف) توزیع متناسب با نیروهای جانبی حاصل از تحلیل دینامیکی خطی طیفی با لحاظ آن تعداد مودهای ارتعاشی که حداقل 90% جرم سازه در تحلیل مشارکت کند.
ب) توزیع بار یکنواخت، که عبارت است از توزیعی متناسب با جرم بدون توجه به ارتفاع هر طبقه.
بارهای جانبی باید در محل جرمها در مدل اعمال گردند. در ساختمانهای دارای دیافراگمهای صلب این بارها میتواند در مرکز جرم کفها اعمال شود. تاثیر خروج از مرکزیت اتفاقی نیز باید اعمال گردد.
- منحنی ظرفیت یعنی رابطه بین برش پایه و تغییرمکان نقطه کنترل باید توسط روش تحلیل استاتیکی غیرخطی از مقدار صفر تا تغییرمکانی معادل 150% تغییرمکان هدف تعیین گردد.
مرکز جرم بام باید به عنوان محل نقطه کنترل اختیار گردد. بام خرپشته را نباید به عنوان نقطه کنترل در نظر گرفت.
منحنی ظرفیت باید تبدیل به منحنی چندخطی گردد تا برش پایه جاری شدن مؤثر سازه و تغییرمکان نظیر آن تعیین و از این مقادیر برای محاسبه زمان تناوب اصلی مؤثر استفاده شود.
چند خطی کردن منحنی ظرفیت، به نحوی صورت میپذیرد که خط اول از نقطه شروع با شیبی برابر با سختی جانبی مؤثر رسم میگردد. سختی جانبی مؤثر برابر سختی سکانت محاسبه شده در برش پایه نظیر 60% برش پایه جاری شدن مؤثر سازه در منحنی ظرفیت است. برش پایه جاری شدن مؤثر سازه نباید از حداکثر برش پایه در نقاط مختلف منحنی ظرفیت بیشتر باشد.
خط دوم نماینده شیب مثبت بعد از جاری شدن سازه است که از نقطهای به مختصات ( دلتاd و Vd) و نقطهای روی خط اول چنان ترسیم میشود که سطح زیر مدل رفتار دو خطی برابر سطح زیر منحنی رفتار غیرخطی تا نقطه( دلتاd و Vd) باشد.( دلتاd و Vd) روی منحنی ظرفیت سازه در تغییرمکان هدف یا در تغییرمکان نظیر برش پایه حداکثر، هر کدام که کمتر باشد، قرار دارد.
خط سوم نماینده شیب منفی بعد از افت مقاومت است که از نقطه انتهای شیب مثبت در منحنی ظرفیت ( دلتاd و Vd)و نقطهای که در آن برش پایه به 60% پایه جاری شدن مؤثر سازه نزول میکند، میگذرد.
پیشنهاد مطالعاتی:
مقاله طراحی سازه بر اساس عملکرد چیست؟ بررسی جامع مفاهیم به همراه ویدیو
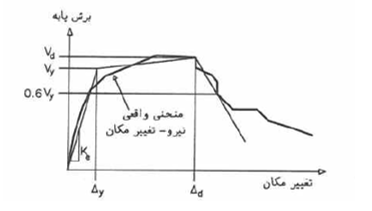
شکل 3- چند خطی کردن منحنی ظرفیت
- زمان تناوب اصلی مؤثر ساختمان، با رابطه زیر محاسبه میشود:
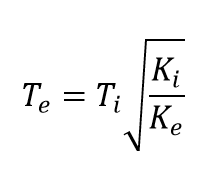
که در آن Ti (بر حسب ثانیه) زمان تناوب اصلی ارتجاعی است، که با تحلیل مدل سازه با فرض رفتار خطی به دست میآید، Kiسختی جانبی ارتجاعی سازه ( شیب خط مماس بر منحنی ظرفیت سازه در مبدأ ) در جهت مورد نظر و Keسختی جانبی مؤثر سازه در جهت مورد نظر میباشد.
- ضریب اضافه مقاومت برابر نسبت برش پایه در هنگام تشکیل سازوکار خمیری کلی در سازه به برش پایه در هنگام تشکیل اولین مفصل پلاستیک میباشد. در روش تحلیل استاتیکی غیرخطی، برش پایه در هنگام تشکیل سازوکار خمیری کلی برابر برش پایه جاری شدن مؤثر سازه فرض میشود. در این روش برای تعیین ضریب اضافه مقاومت، باید کمترین ضریب حاصل از دو توزیع بار جانبی، اختیار شود.
- مقدار تغییرمکان هدف در نقطه کنترل باید با استفاده از روشهای معتبر محاسبه شود. این مقدار را میتوان از رابطه زیر محاسبه نمود.
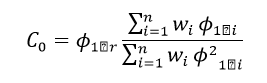

جامعترین دوره آموزش طراحی سازه پروژه محور برای بازار کار
طراحی سازه
- در مورد ساختمانهای (انعطافپذیر پیچشی) که پیچش در مود اول یا دوم آنها حاکم باشد، الگوهای متداول تحلیل استاتیکی غیرخطی میتوانند موجب تخمین کمتر از واقع تغییرمکانها در سمت سخت (مقاوم) ساختمان گردند. در مورد چنین ساختمانهایی تغییرمکانهای سمت سخت (مقاوم) آنها باید در مقایسه با ساختمانهای متعادل پیچشی افزایش یابد. درصورتی که از ضریب بزرگ نمایی برای تغییرمکانهای سمت سخت (مقاوم) استفاده گردد، شرایط مورد نظر این بند را میتوان اقناع شده فرض نمود. این ضریب بزرگ نمایی میتواند از تحلیل خطی دینامیکی طیفی مدل سه بعدی ساختمان بدست آید.
- طراحی سازه باید به نحوی انجام شده باشد که مقاومت سازه در نقطه رسیدن به تغییرمکانی معادل 125 درصد تغییرمکان هدف، کمتر از برش پایه جاری شدن مؤثر سازه نباشد.
حداکثر تغییرمکام نسبی سازه در تغییرمکان هدف نباید بیشتر از 120% مقادیر مجاز معرفی شده در این استاندارد باشد.
کنترل مقاومت اعضا در خصوص تلاشهای کنترلشونده توسط تغییرشکل، با توجه به بازتابهای حاصل از تحلیل ضروری نیست. در مورد آن دسته از تلاشها که کنترل آنها با توجه به ضرایب اضافه مقاومت در روشهای تحلیل خطی ضروری است، مقادیر تلاشهای حاصل از تحلیل غیرخطی در تغییرمکان هدف را باید بدون ضرب کردن در ضریب اضافه مقاومت مورد استفاده قرار داد. در صورتی که این تلاشها از ظرفیت کرانه پایین آنها بیشتر نباشد، قابل قبول تلقی میگردد.
ارزیابی کفایت اعضا و اتصالات در تحمل تغییرشکلها و نیروهای نیاز لرزهای بر اساس نتایج مطالعات آزمایشگاهی برای مدلهای مشابه آن اعضا و اتصالات انجام گردد. تغییرشکل عضوی که وظیفه تحمل بار ثقلی را دارد نباید بیشتر از هر یک از مقادیر زیر باشد: الف) دو سوم تغییرشکلی که در آن عضو ظرفیت باربری ثقلی را از دست میدهد، و ب) دو سوم تغییرشکلی که در آن مقاومت عضو به کمتر از 70 درصد مقاومت حداکثر آن افت میکند. در مورد تغییرشکل عضوی که وظیفه باربری ثقلی ندارد، کافیست شرط (ب) برآورده شود. بجای انجام مطالعات آزمایشگاهی میتوان از روابط معیار پذیرش ایمنی جانی در نشریه 360 معاونت برنامهریزی و نظارت راهبردی نیز برای تعیین ظرفیت تغییرشکل اعضا استفاده نمود.
- اگر ضریب از مقدار ضریب رفتار سازه تقسیم بر ضریب اضافه مقاومت سازه بیشتر باشد، سازه طراحی شده باید به تأیید شخص حقیقی یا حقوقی مستقل باصلاحیت رسانده شود. در این بررسی، موارد زیر باید مورد توجه قرار گیرد.
الف) سازگاری مشخصات سازه با دادههای بکار برده شده در مدل تحلیلی،
ب) سازگاری ظرفیتهای اعضای سازه با نتایج بدست آمده از تحلیل.
پیشنهاد مطالعاتی:
مقاله ضریب رفتار ساختمان در طراحی سازه و پارامترهای مؤثر در آن
تحلیل دینامیکی غیرخطی
تحلیل دینامیکی غیرخطی، که اغلب به آن تحلیل تاریخچه زمانی غیرخطی نیز گفته میشود، تکنیکی پیچیده تر از تحلیل استاتیکی غیرخطی است. تحلیل دینامیکی غیرخطی با استفاده از فرآیند حل گام به گام معادله اصلی حرکت انجام میشود:

علاوه بر پارامترهای ورودی مورد نیاز برای انجام تحلیل استاتیکی غیرخطی، تحلیل دینامیکی غیرخطی نیز به تاریخچه شتاب زمین مناسب و تعریف کامل رفتار هیسترتیک المان ها، از جمله رفتارهای باربرداری و سیکلی نیاز دارد.
مزیت اصلی تحلیل دینامیکی غیرخطی نسبت به تحلیل استاتیکی غیرخطی این است که در این تحلیل، از تقریبهای مرتبط با انتخاب الگوی بارگذاری و راهحل برای جابجایی هدف اجتناب شده و اثرات مود بالاتر و تخریب سیکلی را میتوان مستقیماً در تحلیل لحاظ نمود. با این حال، با توجه به میزان دقت المان هیسترتیک و حرکات زمین پیشبینیهای پاسخ بهدستآمده با تحلیل دینامیکی لزوماً دقیقتر از پیشبینیهای بهدستآمده از تحلیل استاتیکی نیست.
در بند 4 از پیوست دوم استاندارد 2800 درباره تحلیل دینامیکی غیرخطی صحبت شده است:
- در این روش، تحلیل دینامیکی سازه با اثر دادن شتاب زمین به صورت تابعی از زمان در تراز پایه و محاسبه پاسخ مدل ریاضی سازه که در بر گیرنده رفتار فرا ارتجاعی آن است، انجام میشود. مدل مذکور عمدتاً باید با توجه به ضوابط بندهای 1 و 2 پیوست دوم استاندارد 2800 تهیه شده باشد. در این مدل تکیهگاه سازه میتواند صلب فرض شود. استفاده از فرضهای مناسب در خصوص سختی و ظرفیت باربری پی با توجه به ویژگیهای خاک و در نظر گرفتن تکیهگاه انعطافپذیر برای سازه نیز مجاز است.
- شتابنگاشتهایی که در تعیین اثر حرکت زمین مورد استفاده قرار میگیرند باید تا حد امکان نمایانگر حرکت واقعی زمین در محل احداث بنا، در هنگام وقوع زلزله، باشند. برای نیل به این هدف لازم است حداقل سه زوج شتابنگاشت متعلق به مؤلفههای افقی سه زلزله ثبت شده که دارای ویژگیهای مذکور در بند (1-3-5-2) استاندارد 2800 باشند، انتخاب گردند. در مواردی که تعداد مورد نیاز از زوج شتابنگاشتهای مناسب ثبت شده در دسترس نباشد، میتوان از زوج شتابنگاشتهای شبیهسازی شده مناسب برای تکمیل تعداد آنها استفاده کرد. زوج شتابنگاشتهای انتخاب شده باید به روش مذکور در بند (2-3-5-2) استاندارد 2800 به مقیاس درآورده شوند. لیکن در این محاسبات، طیف طرح باید طیف طرح استاندارد تعریف شده در بند (2-1-4-2) استاندارد 2800 بدون اعمال عکس ضریب رفتار در نظر گرفته شود.
- در این تحلیل، اثر زلزله در دو امتداد افقی با استفاده از زوج شتابنگاشتها اعمال میشود. ضمناً لازم است در هنگام اثر زلزله بارهای ثقلی نیز مطابق بند 1 پیوست دوم استاندارد 2800 به مدل سازه اعمال شود. اثر نیز در انجام این تحلیل باید در نظر گرفته شود.
پیشنهاد مطالعاتی:
مقاله انواع میراگر در سازهها: کاربرد، مزایا و مقایسه مدلها
تبصره:
در مورد ساختمانهای منظمی که دارای یک یا چند ستون مشترک بین دو یا چند قاب سیستم باربر جانبی در جهات مختلف نباشند، میتوان تحلیل را در هر امتداد اصلی افقی بطور مستقل انجام داد. در این حالت شتابنگاشتهای انتخاب شده باید شرایط مذکور را دارا باشند، لیکن در مقیاس نمودن آنها دیگر نیازی به تهیه طیف جذر مجموع مربعات زوج مؤلفهها نبوده و شتابنگاشتهای انتخابی باید با مقایسه طیف پاسخ آنها با طیف طرح مقیاس شوند.
- در تحلیل تاریخچه زمانی بازتاب نهایی سازه شامل تلاشهای ایجاد شده در اعضا، تغییرشکل اعضا و تغییرمکان جانبی نسبی طبقات در هر لحظه برابر با حداکثر بازتابهای بدست آمده از تحلیل با سه زوج شتابنگاشت اعمالی به سازه میباشد. در این روش تحلیل، در صورت استفاده از حداقل هفت زوج شتابنگاشت میتوان مقدار متوسط بازتابهای بدست آمده از آنها را به عنوان بازتاب نهایی تلقی کرد.
مقاومت اعضا:
در این روش کنترل مقاومت اعضا در خصوص تلاشهای کنترلشونده توسط تغییرشکل، با توجه به بازتابهای حاصل از تحلیل ضروری نیست. در مورد آن دسته از تلاشها که کنترل آنها با توجه به ضرایب اضافه مقاومت در روشهای تحلیل خطی ضروری است، مقادیر تلاشهای حاصل از تحلیل غیرخطی را باید بدون ضرب کردن در ضریب اضافه مقاومت مورد استفاده قرار داد. در صورتی که این تلاشها از ظرفیت کرانه پایین آنها بیشتر نباشد، قابل قبول تلقی میگردد.
تغییرشکل اعضا:
ارزیابی کفایت ظرفیت اعضا و اتصالات در تحمل تغییرشکلها و نیروهای نیاز لرزهای بر اساس نتایج مطالعات آزمایشگاهی برای مدلهای مشابه آن اعضا و اتصالات انجام گردد. تغییرشکل عضوی که وظیفه تحمل بار ثقلی را دارد نباید بیشتر از هر یک از مقادیر زیر باشد:
الف) دو سوم تغییرشکلی که در آن عضو ظرفیت باربری ثقلی را از دست میدهد،
ب) دو سوم تغییرشکلی که در آن مقاومت عضو به کمتر از 70 درصد مقاومت حداکثر آن افت میکند.
توجه:
در مورد تغییرشکل عضوی که وظیفه باربری ثقلی ندارد کافیست شرط (ب) برآورده شود. بجای انجام مطالعات آزمایشگاهی میتوان از روابط معیار پذیرش ایمنی جانی در نشریه 360 معاونت برنامهریزی و نظارت راهبردی نیز برای تعیین ظرفیت تغییرشکل اعضا استفاده نمود.
تغییرمکان جانبی نسبی طبقات:
تغییرمکان جانبی نسبی طبقات حاصل از تحلیل غیرخطی نباید از 120% مقدار مجاز معرفی شده در بند (3-5-2) استاندارد 2800 تجاوز نماید.
- سازه طراحی شده بر اساس تحلیل تاریخچه زمانی غیرخطی باید به تأیید شخص حقیقی یا حقوقی مستقل باصلاحیت رسانده شود. در این بررسی، موترد زیر مورد توجه قرار گیرد.
الف) شتابنگاشتهای بکار گرفته شده در تحلیل،
ب) سازگاری مشخصات سازه با دادههای بکار برده شده در مدل تحلیلی،
پ) سازگاری ظرفیتهای اعضای سازه با نتایج بدست آمده از تحلیل.
آموزش طراحی اتصالات (پیچی و جوشی) در سازه فولادی
طراحی سازه
مفهوم سختی برای تحلیل الاستیک و غیرالاستیک:
سختی برای تحلیل الاستیک
اگر نیروی وارد بر یک المان از نیروی تسلیم آن تجاوز نکند، فرض معمول برای تحلیل این است که رفتار اساساً خطی و الاستیک است. تنها پارامتری که برای این المان مورد نیاز است سختی آن است.
تیرها، ستون ها و دیوارها دارای سختی محوری، خمشی و برشی هستند. برای تیرها و ستونها، سختی خمشی معمولاً مهمترین ویژگی است. برای دیوارها و همچنین برای تیرهای عمیق، سختی برشی میتواند اهمیت بیشتری داشته باشد.
سختی برای تحلیل غیرالاستیک
اگر نیروی وارد بر یک المان از نیروی تسلیم بیشتر شود، رفتار غیرالاستیک و در نتیجه غیرخطی است. در طراحی مقاوم در برابر زلزله، رفتار غیرالاستیک اغلب برای زلزلههای بزرگ و نادر مجاز است. برای سایر انواع بار، رفتار غیر کشسان ممکن است به صراحت مجاز نباشد، اما اگر بارهای وارده بر سازه از بارهای طراحی بیشتر شود، این احتمال وجود دارد.
در نظر گرفتن رفتار غیرالاستیک به طور مستقیم در یک مدل تحلیل ضروری نیست، حتی برای طراحی مقاوم در برابر زلزله. جنبه منفی تحلیل غیرالاستیک این است که یک مدل تحلیل غیرالاستیک نه تنها به سختی المان ها بلکه به ویژگی هایی مانند مقاومت، سختی کرنشی، شکل پذیری و شکل منحنی هیسترزیس نیز نیاز دارد. همچنین، تحلیل غیرخطی به زمان بسیار بیشتری نسبت به تحلیل الاستیک خطی نیاز دارد. نکته مثبت این است که تحلیل غیرالاستیک می تواند اطلاعات بهتری را برای طراحی نسبت به تحلیل الاستیک ارائه دهد. تجزیه و تحلیل الاستیک حتی ممکن است اطلاعات گمراهکنندهای را ارائه دهد.
رفتار غیر خطی مواد (Material nonlinearity)
غیرخطی بودن مواد با رفتار غیرالاستیک یک المان یا سیستم مرتبط است. رفتار غیرالاستیک ممکن است با یک رابطه نیرو-تغییرشکل (F-D) مشخص شود که به عنوان منحنی Backbone نیز شناخته میشود، که مقاومت را در برابر تغییر شکل انتقالی یا چرخشی اندازهگیری می کند.
نمودار F-D
منحنی هیسترزیس یک حالت توسعه یافته از نمودار نیرو-جابجایی است، لذا لازم است مروری بر مفاهیم این نمودار شود. این منحنی از بارگذاری یکنواخت (Monotonic)، و منحنی هیسرزیس از بارگذاری سیکلی (رفت و برگشتی) بدست می آید. برای بسیاری از المان ها رابطه نیرو-تغییر شکل (F-D) به صورت نمودار زیر است. شکل کلی منحنی F-D برای المانهای مختلف مشابه است.
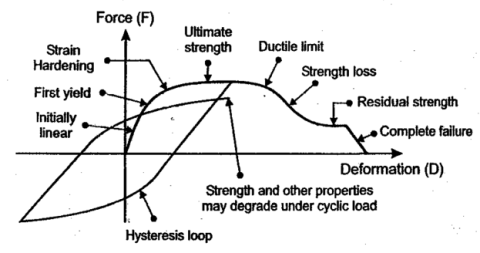
شکل 3 – یک نمونه متداول منحنی F-D
پیشنهاد مطالعاتی:
مقاله مقاوم سازی با FRP
منحنی نیرو-جابجایی برای یک المان می تواند ویژگی های زیادی داشته باشد. لازم نیست همه این ویژگی ها را برای همه ی تجزیه و تحلیل ها مشخص شود. سه دسته کلی از تحلیل وجود دارد که به ویژگی های پیچیده تری نیاز دارند که به شرح زیر است.
- الاستیک خطی: سختی ثابت را فرض میکند. این رایج ترین نوع تحلیل است. برای محاسبه تقاضای مقاومت، برای مقایسه ظرفیتهای مقاومت استفاده می شود.
- غیرخطی غیرسیکلی (غیرخطی یکنواخت)، که معمولاً غیرالاستیک است اما می تواند غیرخطی الاستیک باشد. این حالت به یک رابطه غیرخطی F-D نیاز دارد اما به یک حلقه هیسترزیس نیاز ندارد. چند مورد از کاربردهای این دسته شامل این موارد است: (الف) محاسبه ظرفیت مقاومت برای یک سازه یا مجموعه سازه، (ب) تحلیل پوش آور استاتیکی برای ارزیابی عملکرد تحت بارهای زلزله، (ج) خرابی پیشرونده، تحلیل خرابی سازه های آسیب دیده در اثر انفجار. برای این مورد آخر می توان از تحلیل استاتیکی یا دینامیکی استفاده شود. در یک تحلیل دینامیکی، رابطه F-D باید بارگذاری-باربرداری مجدد را در نظر بگیرد، اما معمولاً تغییر شکل سیکلی غیرکشسانی وجود ندارد.
- غیر خطی سیکلی: این معمولاً غیرالاستیک است و به حلقه های منحنی هیسترزیس نیاز دارد. رایج ترین کاربرد آن تحلیل دینامیکی برای بارهای زلزله است.
منحنی هیسترزیس
تا اینجا با لزوم استفاده از منحنی های هیسترزیس آشنا شدیم. هنگامی که یک المان تحت بارگذاری سیکلی قرار میگیرد، منحنی رابطه F-D برای یک المان از یک حلقه هیسترزیس پیروی می کند.
حالات مختلف منحنی هیسترزیس
با توجه به شکل 3 در ادامه ی منحنی F-D تحت بارگذاری سیکلی، چند مورد از حالات منحنی هیسترزیس در شکل 4 آورده شده است که برای هر حالت توضیحات هم ارائه شده است.
- شکل (a) یک حلقه کامل را نشان میدهد، که در آن، شکل حلقه مانند شکل رابطه اصلی F-D است.
- شکل (b) حلقه ای را نشان میدهد که دارای stiffness degradationاست. در این حلقه، سختی بارگذاری-باربرداری کوچکتر از سختی در رابطه اصلی F-D است. مساحت حلقه برابر است با مقدار انرژی غیرکشسانی است که در اثر تغییر شکل سیکلی تلف میشود. حلقه در شکل (b) دارای مساحت کوچکتری نسبت به شکل (a) است، بنابراین کاهش سختی منجر به کاهش انرژی میشود.
- شکل (c) یک حلقه Pinched را نشان می دهد، در این وضعیت مقاومت المان تغییری نمیکند بلکه قابلیت جذب انرژی آن کاهش پیدا میکند.
- همانطور که در شکل (d) نشان داده شده است، ممکن است در منحنی strength degradation و همچنین stiffness degradation وجود داشته باشد و با افزایش سیکل ها کاهش هر دو این پارامترها ممکن است به تدریج توسعه یابد.
- از شکل (e) نیز برداشت می شود که با افزایش سیکل ها ممکن است مقاومت افزایش یابد.
- همانطور که در شکل (f) نشان داده شده است، Degradation ممکن است باعث کاهش مقاومت شود. با معکوس کردن جهت بارگذاری ممکن است مقاومت جهت معکوس کاهش یابد. برای مثال، فرض کنید که یک تیر بتن آرمه به دلیل له شدن تحت اثر فشار در پایین تیر و با ترک خوردن در بالای تیر، مقاومت خود را از دست دهد. هنگامی که تغییر شکل خمشی معکوس می شود، ترکها در بالای تیر بسته می شوند و بتن تحت فشار قرار می گیرد. از این رو، خرد شدن بتن در یک جهت ممکن است تأثیر کمی بر مقاومت خمشی در جهت دیگر داشته باشد. (این تغییرات ممکن است تأثیرگذار باشد، زیرا بتن ترک خورده است و ممکن است در هنگام بسته شدن ترکها از نظر فشاری مقاوم نباشد. همچنین، آرماتور بالایی احتمالاً در کشش تسلیم شده است و ممکن است وقتی تحت فشار قرار میگیرد، کمانش کند. این نشان دهنده رفتار پیچیده ای است که میتواند تحت تغییر شکلهای سیکلی رخ دهد).
- اثر تغییر شکل های سیکلی در شکل (g) نشان داده شده است. این شکل رابطه منحنی F-D را برای المانی که فقط به صورت یکنواخت بارگذاری میشود و همچنین رابطه موثر پس از اینکه المان تحت چندین سیکل تغییر شکل قرار گرفت را نشان می دهد. تغییر شکل سیکلی میتواند استحکام قطعه و همچنین شکل پذیری آن را کاهش دهد. این اثر معمولاً پیش رونده خواهد بود و با افزایش تعداد سیکلها، میزان تخریب افزایش می یابد.
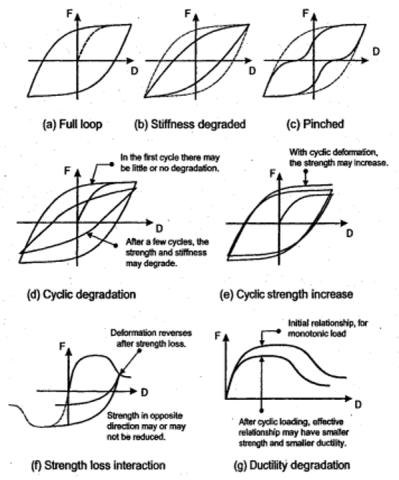
شکل 4 – حالات مختلف تغییر سیکلی منحنی هیسترزیس
تغییرشکلهای الاستیک و پلاستیک
منحنی F-D برای یک المان، اغلب دارای یک ناحیه ی خطی اولیه است که در آن رفتار الاستیک است. هنگامی که یک المان فراتر از محدوده الاستیک بارگذاری می شود، تغییر شکل آن معمولاً به عنوان بخشی الاستیک و تا حدی پلاستیک در نظر گرفته می شود، همانطور که در شکل زیر نشان داده شده است. رابطه F-D در شکل زیر در ابتدا خطی است و دارای یک نقطه تسلیم نسبتاً مشخص است. تغییر شکل الاستیک برابر با تقسیم نیروی متناظر بر سختی اولیه است. تغییر شکل پلاستیک نیز برابر است با اختلاف کل تغییر شکل و تغییر شکل الاستیک. این شکل همچنین تغییر شکل پس از تسلیم را نشان می دهد که تا حدودی بزرگتر از تغییر شکل پلاستیک است.
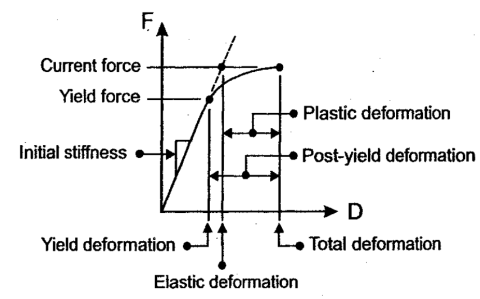
شکل 5 – تغییرشکلها در منحنی F-D
در شکل قبلی تغییر شکلها را برای افزایش یکنواخت تغییر شکل نشان داده شد، شکل زیر نمونه ای با تغییر شکل سیکلی را نشان میدهد.
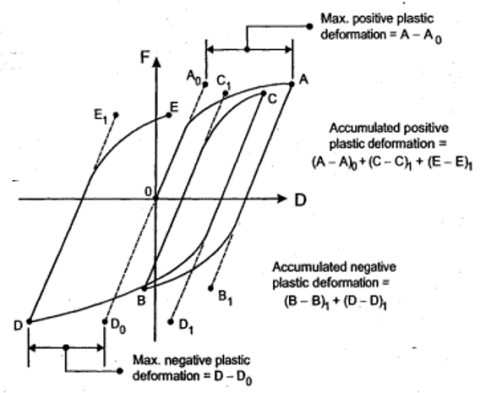
شکل 6 – تغییرشکلهای پلاستیک در منحنی هیسترزیس
در این مثال تغییر شکل ها در طول مسیر 0-A-B-C-D-E سیکل ها طی می شود. همانطور که نشان داده شده است، حداکثر تغییر شکل ای پلاستیک مثبت و منفی از خط الاستیک اصلی اندازه گیری می شود. تغییر شکل های پلاستیک تجمعی برای هر تغییرات سیکلی محاسبه می شود. تغییر شکل های انباشته شده مثبت و منفی ممکن است برای به دست آوردن یک تغییر شکل انباشته کل اضافه شوند.
برای ارزیابی عملکرد یک المان که اجازه تسلیم شدن را دارد، تغییر شکل پلاستیک یک معیار برای بدست آوردن رابطه ی ظرفیت-تقاضا مشهود است.
انواع رفتار منحنی هیسترزیس
شکل 7 چندین مدل متداول هیسترتیک را نشان میدهد. که در ادامه توضیح داده خواهد شد.
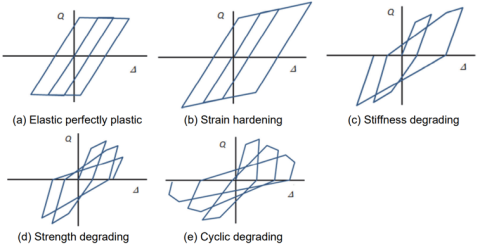
شکل 7 انواع رفتار منحنی هیسترزیس
- شکل (a): (Elastic-Perfectly-Plastic) یک رفتار ایده آل که در آن بارگذاری اولیه باعث ایجاد تغییر شکل با نرخ سختی ثابت می شود، تا زمانی که نیروی اعمال شده با مقاومت تسلیم المان برابر شود، که در آن نقطه المان تحت این نیروی ثابت به تغییر شکل پلاستیک، در سختی صفر ادامه می دهد. هنگامی که نیروی اعمال شده کاهش می یابد، المان تغییر شکل را با همان نرخ سختی تجربه شده در بارگذاری اولیه بازیابی می کند تا زمانی که نیرو معکوس شود و دوباره به سطح تسلیم برسد، در این زمان تغییر شکل پلاستیک معکوس تحت نیروی ثابت رخ می دهد. سختی بارگذاری الاستیک و مقاومت تسلیم بدون توجه به تعداد سیکل های حرکت یا بزرگی تغییر شکل تحمیلی ثابت می ماند.
- شکل (b): (Strain Hardening) رفتاری شبیه به شکل a، با این تفاوت که پس از مقاومت تسلیم المان شروع به تغییر شکل بیشتر در سختی مثبت و غیر صفر می کند. تحت سیکل های متوالی بارگذاری، در هر جهت بارگذاری مقاومت تسلیم همواره بزرگتر از مقاومت تسلیم سیکل قبلی است. این شکل از منحنی هیسترزیس نشان دهنده رفتار برخی از عناصر فولادی قبل از شروع کمانش یا شکستگی است.
- شکل (c): (Stiffness Degrading) رفتاری مشابه رفتار شکل c، با این تفاوت که پس از بارگذاری مجدد، تغییر شکل در سختی کاهش یافته رخ میدهد. کاهش سختی در نتیجه آسیب هایی است که رخ داده است، مانند ترک در دیوارهای بتنی یا بنایی.
- شکل (d): (Strength Degrading) رفتاری مشابه رفتار شکل c، با این تفاوت که هر سیکل متوالی حرکت شروع به تسلیم در سطح نیروی کمتری رخ میدهد. مانند Stiffness Degrading، کاهش مقاومت تسلیم را میتوان به آسیب هایی مانند خرد شدن موضعی یا پوسته شدن بتن نسبت داد.
- شکل (e): (Cyclic Degrading) رفتاری مشابه رفتار شکل d، با این تفاوت که در سیکلهای متوالی با کاهش سختی، مقاومت تسلیم افزایش مییابد.
تحلیل غیرالاستیک برای منحنی هیسترزیس
منحنی Backbone
منحنی F-D بدست آمده از آزمایشات، به یک منحنی Backbone تبدیل می شود. می توان از آن برای ساخت یک تقریب چندخطی، منحنی F-D استفاده کرد. همچنین می توان از این منحنی برای ارتباط دادن حلقه های منحنی هیسترزیس نیز استفاده نمود.
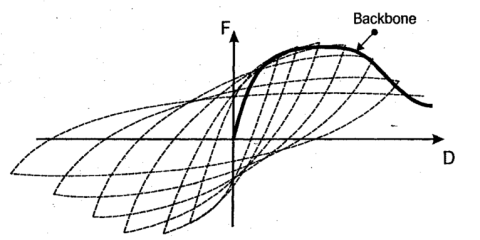
شکل 8 – منحنی Backbone بر اساس منحنی هیسترزیس
یک مسئله کلیدی این است که با افزایش تعداد سیکل های تغییر شکل، بسیاری از المان ها به تدریج تخریب می شوند و از این رو منحنی Backbone به میزان سیکل ها بستگی دارد. به طور خاص، یک رابطه Backbone که تغییر سیکلی را بیان می کند، میتواند به طور قابلتوجهی با رابطه یکنواخت بدون بارگذاری سیکلی متفاوت باشد.
در طول دههها، محققان دهها و احتمالاً صدها مدل مختلف برای منحنی هیسترزیس پیشنهاد کردهاند. برخی نسبتاً ساده هستند و برخی از قوانین هندسی پیچیده پیروی می کنند. یکی از عملی ترین روشها (در واقع، تنها روش عملی) این است که با یک منحنی Backbone نیرو-تغییرشکل شروع شود، و حلقه هیسترزیس به آن رابطه متصل شود. این در شکل 9- زیر نشان داده شده است.
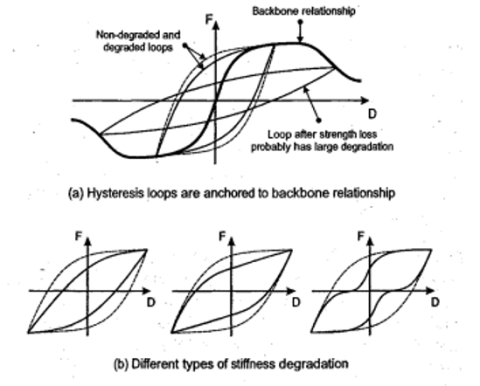
شکل 9 – ارتباط منحنی هیسترزیس و منحنی Backbone
پیشنهاد مطالعاتی:
مقاله مهاربند کمانش تاب (BRB) چیست و چه کاربردی دارد؟
degradation سیکلی باعث می شود با افزایش تعداد سیکل ها، سختی، مقاومت و شکل پذیری کاهش یابد. همچنین ممکن است در degradation in the strain hardening stiffness ، میزان از دست دادن مقاومت پسماند و تغییر شکل در شکستِ کامل کاهش یابد.
برای هر المانی که دارای degradation سیکلی است، همیشه عدم اطمینان زیادی در مورد رفتار وجود خواهد داشت. انتظار دقت در مدل تحلیل را نداشته باشید. عملیترین روش برای مدلسازی degradation سیکلی، استفاده از یک رابطه منحنی Backbone و degradation آن رابطه است. دو رویکرد جایگزین وجود دارد که به شرح زیر است.
- degradation سیکلی را به طور غیرمستقیم در نظر بگیرید. تعداد معینی از سیکلهای تغییر شکل را در نظر بگیرید و یک منحنی Backbone را انتخاب کنید که این سیکلها را شامل شود. این روشی است که در ASCE 41 اتخاذ شده است.
- degradation سیکلی را مستقیماً در نظر بگیرید. یکی از راههای انجام این کار، تعریف یک رابطه مورتوتونیک (mortotonic) است که زمانی اعمال میشود که بارگذاری سیکلی وجود ندارد، و یک رابطه fully degraded که پس از سیکلهای زیاد اعمال میشود. این در شکل زیر نشان داده شده است. مقاومت، شکل پذیری و مقاومت پسماند ممکن است همگی کاهش پیدا کنند. لازم است یک قانون درون یابی تعریف شود که مشخص کند چگونه رابطه Backbone با افزایش سیکل ها تغییر میکند.
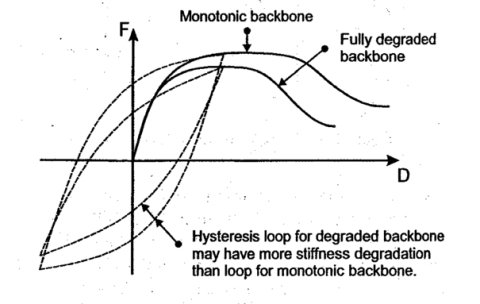
شکل 10 – منحنی Backbone و منحنی با بارگذاری یکنواخت
نمونه هایی از منحنی هیسترزیس برای اعضای سازهای
در این بخش چند نمونه از منحنی های هیسترزیس انواع سیستم های سازه ای آورده شده است.
قاب خمشی فولادی
شکل زیر نمودارهای چرخش-ممان را برای اتصالات تیر-ستون قاب خمشی ویژه فولادی که در معرض سه تاریخچه بارگذاری مختلف قرار دارند، نشان میدهد. قابهای خمشی فولادی یکی از انعطافپذیرترین عناصر مقاوم در برابر نیروی لرزهای با پاسخ سیکلی هستند که معمولاً با حلقههای هیسترزیس عریض نشان داده میشوند.
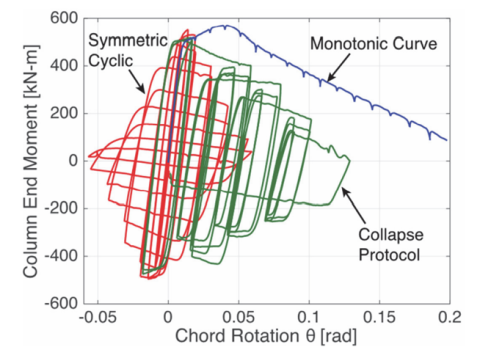
شکل 11 – مونتاژ قاب خمشی فولادی تحت پروتکل های بارگذاری جایگزین (Suzuki و Lignos، 2015)
قاب فولادی با مهابربند همگرا
شکل زیر رفتار هیسترزیس مهاربندها را نشان میدهد که با کمانش در فشار، تسلیم شدن در کشش، و در نهایت شکست، کنترل میشود، که معمولاً در نقطه مفصل پلاستیک در طول وسط مهاربند که همراه با کمانش است، شروع میشود.
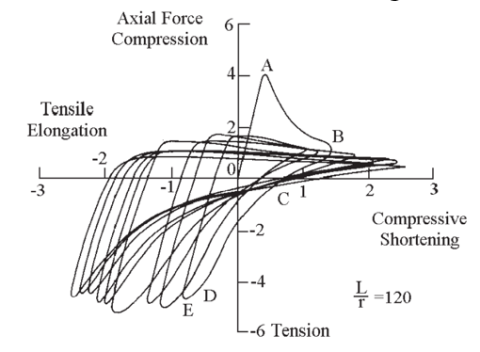
شکل 12 – منحنی هیسترزیس قاب فولادی خمشی معمولی
پیشنهاد مطالعاتی:
مقاله آموزش طراحی مهاربند همگرای فولادی (گام به گام+مثال عملی)
قاب خمشی بتنی
شکل زیر پاسخ هیسترتیک سیکلی مجموعههای ستون تیر را نشان میدهد که با طراحی SMF، همراه با مدلهای هیسترتیک تحلیلی معمول اعمال میشوند. همانطور که در شکل نشان داده شده است، پاسخ سیکلی شامل pinching متوسط، یک محدوده پلاستیک پایدار و به دنبال آن کاهش قدرت است.
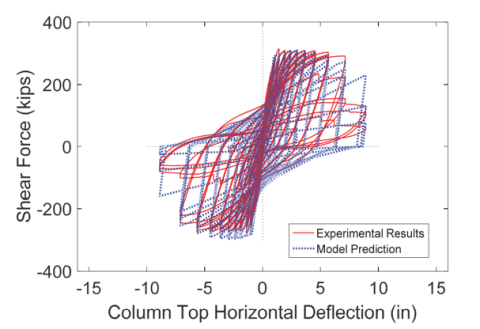
شکل 13 – رفتار هیسترزیس و مدل سازی مجموعه تیر-ستون قاب خمشی ویژه بتن مسلح (نجوان و همکاران، 2014).
منابع:
- استاندارد 2800، ویرایش چهارم.
- بسته آموزشی پاراپلاس، مهندس امیرطه نوروزی.
- Wilbur L. Ross, Jr., Secretary; Recommended Modeling Parameters and Acceptance Criteria for Nonlinear Analysis in Support of Seismic Evaluation, Retrofit, and Design
- Graham H. Powell; Modeling for Structural Analysis
- Material nonlinearity – Technical Knowledge Base, CSI America.



